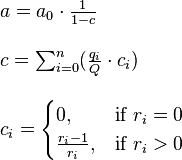Large Battle Algorithm
High Level Overview
Ships are no longer handled individually. Instead, ships are grouped by their type and what percentage of hull they have remaining. We calculate all the rapidfire shots upfront, then split them across the ship groups. Then we process damage on each group individually, given all the incoming shots and their attack powers. Ships are moved into other groups as their hull decreases.
Example Battle
ATTACKERS 1000000 x prometheus 1000000 x hades 136291 x ares 1000000 x athena 300000 x poseidon 1 x dionysus 8904562 x apollo 20000000 x artemis
DEFENDERS 2744694 x artemis 2399622 x atlas 1250719 x apollo 1035136 x zagreus 823126 x hercules 489903 x dionysus 355051 x poseidon 184235 x athena 97041 x ares 100013 x hades 83854 x prometheus 429 x zeus 6537202 x missile turret 5736135 x laser turret 1481787 x pulse cannon 1209407 x particle cannon 295426 x gauss cannon 61795 x plasma turret 1 x decoy 1 x large decoy
---
In the original algorithm, every single one of these ships would be tracked individually. In the new algorithm, we track them in groups instead.
---
At the start of the round, each group of ships attacks. In the old algorithm, that meant each individual ship got to attack, and if it rapidfired, it attacked again, etc., looping until it failed a rapidfire check. In the new algorithm, we use a single equation to calculate the total number of shots that will be fired beforehand, and then we distribute them across the enemies after.
where a is the final number of attacks
this is the closed form of a geometric series as it converges on infinity
where a0 is the initial number of attacks, taking into account multifire, if any c represents the total chance that any shot will rapidfire, given all the enemy ships where Q is the total number of enemy ships where n is number of types of enemy ships where qi is the number of a specific type of enemy ship where ri is the rapid fire rating against a specific type of enemy ship
So if the attacker's prometheus are firing, we get:
a0 = 1000000
to calculate c:
c = 0.209459800751254
and:
a = 1264957.81106426
this final number is then randomized a bit:
g = gaussian random number final shots = a + 0.2 * g * a
final shots is not permitted to be less than a0
---
These shots are then divided semi-randomly amongst the enemies in rough proportion to qi / Q:
x0 is initially set to final shots For each target, i
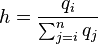
g = a new gaussian random number times hit = x + x * (d / x) * g x = x - times hit
---
Each ship attacks in this way. At this point we are merely tallying the hits for the round. No actual damage is applied.
---
After all the hits have been tallied, we apply the damage.
Now, let's say the defender's atlas took the following hits:
30286 from ares at 1000 damage 96516 from athena at 1000 damage 111444 from hades at 700 damage 910988 from apollo at 150 damage 43874 from poseidon at 400 damage 1928660 from artemis at 50 damage 125166 from prometheus at 2000 damage
The first thing we do is strip out any bounced attacks (less than 1% of the shield rating). In the case of our atlas, nothing is removed.
Then, as an optimization, we merge any attacks that are big enough to kill the ship in one hit into a single group. We also truncate that damage down to the maximum meaningful amount that can be dealt.
910988 from apollo at 150 damage 1928660 from artemis at 50 damage 407286 at 400 damage
---
Now, instead of tracking every ship's hull individually, which can take gigabytes of memory at the upper levels, we instead make 20 buckets representing what percentage of hull is remaining for the ships in the bucket:
[dead, 0~5%, 5~10%, 10~15%, ..., 85~90%, 90~95%, 95~100%] We chose 20 buckets (+ the dead one) at 5% each because, experimentally, increasing it further did not improve accuracy much while it did make it take significantly longer to run. Now, there's probably some room for further optimization here, as, for example, an atlas requires very few buckets to model, while a zeus might require more.
---
At the start of the battle, our defender's atlas looks like this: [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 2399622] 2399622 total In other words, all the ships start in the 95~100% hull bucket.
For each bucket, we also track the average shield of a ship in that bucket and what percentage of the ships in that bucket have been hit this round.
Ships will be moved down in buckets as damage is applied.
---
Let's take a closer look at what happens when we apply the 910988 attacks at 150 damage from the attacker's apollo.
First we take all the shots and we divvy them into the buckets based on how many ships are in each. Since the battle is just starting, all the shots go in the biggest bucket, since that's where all the ships are.
We then further look in each bucket and apply the shots. In this case, there's only one bucket with shots and ships.
---
So now we apply 910988 attacks at 150 damage to the 2399622 ships in the biggest bucket.
We're now faced with the task of figuring out how many ships are hit 0 times, 1 time, 2 times, and so on. In order to calculate that, we approximate what is called a Probability Mass Function (PMF) using a couple different Probability Distribution Functions (PDF).
If the average number of times the ship is hit is more than 20 times, we approximate using a normally distributed PDF. If it is less than 20, we use a poisson PDF, which is more accurate, but much more expensive to calculate.
When the mean is far enough away from zero, the normal distribution is more than sufficient, but when it is close to zero, we have to use a poisson distribution because a ship cannot be hit a negative number of times, skewing the distribution so that it is not normal.
Where mu is the mean (number of shots / number of ships) sigma is the standard deviation (square root of the mean) and x is index we are calculating (representing number of times hit)
While calculating our PMF, we make the optimization of calculating the minimum number of hits it takes to destroy the ships, and then combining all of the probabilities above that point into a single bucket.
So in the case of the defender's atlas, we get the following (poisson):
0 hits - 68.4109% 1 hit - 25.9714% 2 hits - 4.9299% 3 hits - 0.6878%
We then take the 2399622 ships in this bucket and split them up accordingly:
0 hits - 1641603 1 hit - 623215 2 hits - 118298 3 hits - 16504
error: 0.006798 + 0.428108 + 0.964978 + 0.600116 = 2
We put the fractional error in the most likely place, in this case, 0 hits, bringing it up to 1641605.
Now, for each of these scenarios, we apply the damage using the hull and average shield from the bucket it is in. We take into account piercing at this point.
So:
1641603 ships take no hits, and so remain in the same bucket. 623215 ships take 1 hit, dealing 150 damage, for 140 total hull damage, bringing them down to 250 of 390 hull. 118298 ships suffer 2 hits, dealing 300 damage, for 290 total hull damage, bringing them down to 100 of 390 hull. 16504 ships suffer 3 hits, dealing 450 damage, for 390 total hull damage, bringing them down to 0 of 390 hull.
We are now storing the following: [16504, 0, 0, 0, 0, 118298, 0, 0, 0, 0, 0, 0, 0, 623215, 0, 0, 0, 0, 0, 0, 1641605] 2399622 total
For all buckets but the last, the percent hit is 100% and the average shield is 0. The last bucket has 0% hit and an average shield of 10.
---
We then apply the remaining hits in a similar way, distributing the shots into each bucket based on the number of ships there, then calculating a PMF for each to determine how many ships were hit how many times, then moving them into new buckets based on the damage dealt by the given number of shots.
Note that when we move them into new buckets, we are placing them in a separate data structure, meaning that we do not process hits on the same set of ships multiple times.
1928660 attacks at 50 damage => [40181, 0, 42563, 4882, 0, 77373, 0, 0, 92163, 0, 237007, 0, 0, 342578, 0, 237359, 0, 0, 590641, 0, 734875]
407286 attacks at 400 damage => [408503, 0, 35919, 4121, 0, 65295, 0, 0, 77777, 0, 200008, 0, 0, 289099, 0, 200306, 0, 0, 498438, 0, 620156]
---
Now that all the attacks have been applied, we have ships explode based on their remaining hull and how likely it was that they were hit.
(At this point we also apply automatic self-kills from kamikaze ships and mines)
We take that percentage of ships that was hit from each bucket and apply the chance to explode based on the percentage hull it has based on which bucket it is in. The ones that have 70% hull or higher have no chance to explode.
After applying explosions, we get:
[757505, 0, 2751, 524, 0, 14771, 0, 0, 29327, 0, 95234, 0, 0, 180610, 0, 200306, 0, 0, 498438, 0, 620156]
---
And then, destroying the ships is as simple as clearing out the dead bucket:
[0, 0, 2751, 524, 0, 14771, 0, 0, 29327, 0, 95234, 0, 0, 180610, 0, 200306, 0, 0, 498438, 0, 620156]
And the remaining quantity of ships is 1642117.
---
This data is preserved into the next round, after resetting the average shield and percent hit for each bucket.
---
We apply attacks in that way to every ship, then proceed on to the next round.
Outline
Battle:
Setup:
Players are grouped into factions (attacker or defender)
Factions contain fleets, which are groups of ships
Ships have a type (e.g. athena) and a quantity and an attack strategy
Attack strategies include rapidfire, kamikaze, mine, simple, and none (multifire and piercing are handled elsewhere)
mines have no attack strategy when attacking (shouldn't be possible anyway)
kamikaze have no attack strategy when defending
Execute:
for up to 6 rounds:
apply attack strategies for each type of ship on both sides
putting the resulting hits into the appropriate buckets to be processed after all shots have been fired
process attacks for each attack bucket
Attack buckets:
Setup:
resolution = 20 (for now)
Create slices according to resolution
each slice contains a quantity of ships
the index of each slice represents what percentage of hull a ship has remaining
e.g. 0%, 2.5%, 7.5%, 12.5%, ..., 97.5%
it also stores the average shields of all the ships
as well as what percentage of ships have been hit
initially, all ships are in the last slice, representing (mostly) full hull
Process attacks:
for each attacking type of ship
attacks = how many shots/autokills it took from each other type of ship
as well as the damage a single shot of that type does
(remember, autokills are usually self-kills from kamikaze/mines)
filter out all the attack that bounce due to shields
(optimization) combine all attacks that are big enough to destroy the ship in one hit into a single group
For each incoming attack:
split the number of shots across the slices, according to the proportion of ships in each
for each slice,
calculate a probability mass function
this is an array
where the index is the number of times hit
and the value is the percentage of ships hit that many times
mean = shots / ships
dev = sqrt(mean)
(optimization) last index will contain the sum of all probabilities higher than
((hull + shield) / damage).floor + 1
which is to say, all times-hit that are sufficient to kill a ship
(optimization) we stop calculating on the high end once we have passed the mean and have reached near-0 again
each index of the pmf is estimated by calculating the probability distribution function at that index:
if the mean > 20 (meaning that each ship is hit an average of 20 times or more)
then we use a normal pdf (inexpensive)
(1.0 / (dev*Math.sqrt(2*Math::PI)))*(Math::E**-(((x-mean)**2)/(2.0*dev**2)))
otherwise we use a poisson pdf (expensive)
Math::E**(-mean) * (mean**x) / x.factorial
using the percentages in the pmf, we can figure out how many ships were hit how many times
we then move the ships into new slices, accordingly
here we take into account hull, average shield, and piercing to decide the new bucket
note: this is a separate data structure.
We do not re-process hits on these ships until the next attack is processed
we commit the results
we divvy up the auto-kills in proportion to the number of ships at each slice
and move those into the 0th slice (dead ships)
we then calculate how many ships in each slice explode
applying the chance to explode only to the percentage of ships hit stored in the slice
based on their remaining hull %, which is known by the slice index
(70% or greater hull do not explode)
and based on how likely they were to be hit at least once
and then we move those into the 0th slice (dead ships)
we clear out the dead ships in the 0th slice
and commit the updated ship quantity
finally, we reset the shield & percent hit in the slices
shield to the unit's initial shield
percent hit to 0
Attack strategies:
Returns a hash
key: target hit (usually an enemy, but may be an ally in the case of kamikaze/mines)
value: number of units hit (usual)
and number of units automatically destroyed (used only for kamikaze/mines)
Rapidfire:
calculates the total number of shots that will be fired
calculate the chance that any individual shot might rapidfire:
n = base number of shots fired (1 per attacking ship, unless multifire)
by 'attacking ship' I mean of only one type
t = total number of enemy ships that can be hit
per enemy type of ship:
n = number of enemy ships of this type
r = rapid fire rating of the attacking type of ship vs the defending type of ship
(skip if r is zero)
c = (r-1)/r
h = n / t
total rapid fire chance is the sum of all h * c
shots = 1 / (1 - chance any shot might rapidfire)
at this point we use a gaussian random number to vary shots
use a standard deviation of (0.02 * shots)
shots cannot be less than the number of attacking ships
spread the shots out amongst the enemy ships:
(this spread algorithm is the same for all the attack strategies)
per each enemy type of ship:
calculate number of times hit:
chance = number of enemy ships of this type / remaining unprocessed enemy ships including ships of this type
use a bernoulli standard deviation based on shots and chance
vary shots using deviation
Kamikaze: Same as Simple, but also returns 100% kill for all attacking ships
Mine:
Nothing happens if 5 times as many mines as there attacking ships have already been destroyed
calculate number of mines that exploded:
chance = ln(number of attackers) / 4
maximum of 1
(0.2 * chance * number of mines) rounded
enemy explosions = (0.75 * number of mines exploded) rounded
friendly explosions = the remainder
spread enemy explosions as attacks over enemies (see above)
spread friendly explosions as attacks over allies
return 100% kill for the exploded mines
Simple: number of shots is equal to number of ships (more if multifire) spread shots over enemies (see above)
None: Simply doesn't attack